SYMETRIE
PUNKTY SYMETRYCZNE WZGLĘDEM PROSTEJ
Na początek przypomnijmy sobie, jakie warunki spełniają punkty symetryczne względem prostej.
Jeżeli punkt A nie leży na prostej k, to punkt A' jest symetryczny do punktu A względem prostej k, gdy:
- punkty A i A' leżą po przeciwnych stronach prostej k
- odcinek AA' jest prostopadły do prostej k
- odległość punktu A' od prostej k jest równa odległości punktu A od tej prostej
Jeżeli punkt leży na prostej k to jest symetryczny sam do siebie.
Aby znaleźć figurę symetryczną do wielokąta względem danej prostej, wystarczy najpierw znaleźć punkty symetryczne do wierzchołków wielokąta, a następnie odpowiednio te punkty ze sobą połączyć.
Na powyższym rysunku w ten właśnie sposób została narysowana figura symetryczna do trójkąta ABC względem prostej k.
PUNKTY SYMETRYCZNE WZGLĘDEM DANEGO PUNKTU

Punkt A' jest symetryczny do punktu A względem punktu S, jeżeli:
- punkt A' leży na półprostej AS
- odcinki AS i A'S mają jednakowe długości (punkt S jest środkiem odcinka AA')
Aby znaleźć figurę symetryczną do wielokąta względem danego punktu, wyznaczamy najpierw punkty symetryczne do wierzchołków wielokąta, a następnie odpowiednio je łączymy.
Na powyższym rysunku w ten sposób narysowano trójkąt symetryczny do trójkąta ABC względem punktu O.
PUNKTY SYMETRYCZNE WZGLĘDEM OSI UKŁADU WSPÓŁRZĘDNYCH
OŚ SYMETRII
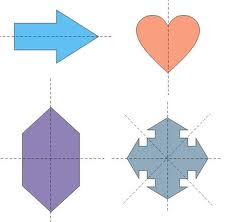
Jeżeli figura jest symetryczna sama do siebie względem pewnej prostej, to tę prostą nazywamy osią symetrii figury, a figurę nazywamy osiowosymetryczną.
ŚRODEK SYMETRII FIGURY
Jeżeli figura jest symetryczna sama do siebie względem pewnego punktu, to ten punkt nazywamy środkiem symetrii figury, a figurę nazywamy środkowosymetryczną (figura obrócona o 180 stopni ma taki sam wygląd jak przed obróceniem).
Jutro kolejny wpis, miłego wieczoru. Pozdrawiamy. Wiki i Ola :)